2019-11-01

数据结构线性结构

words: 1.2k views: time: 5min

算法设计

从百科中可以找到定义：数据结构即计算机存储、组织数据的方式，它的目标是反映数据元素之间的逻辑关系，其中的逻辑关系是指数据元素之间的前后关系，而与他们在计算机中的存储位置无关。

常见的数据结构可以分为四种：

集合：数据结构中的元素之间除了“同属一个集合” 的相互关系外，别无其他关系；
线性结构：数据结构中的元素存在一对一的相互关系；
树形结构：数据结构中的元素存在一对多的相互关系；
图形结构：数据结构中的元素存在多对多的相互关系。

1. 定义

这里要讨论的列表、栈、队列都属于线性结构，区别只在于对插入和删除作了不同的限制。

列表：即所有元素连在一起，其中任意元素节点都可以链接到它的后一个或前一个元素，可以在任意位置进行元素插入或删除。

队列：队列是限制插入和删除必须分别在表的两端进行的表。其基本操作有offer和poll，特点是先进先出。

栈：栈是限制插入和删除都只能在一端进行的表，该位置也叫栈顶。其基本操作有push和pop，特点是后进先出。

2. jdk实现

线性结构其实相对比较容易，就不打算展开赘述了，java集合框架中提供了很多数据结构的实现，下图列出了部分与线性结构相关的类（这里不扩散问题，暂时忽略线程安全相关的类）

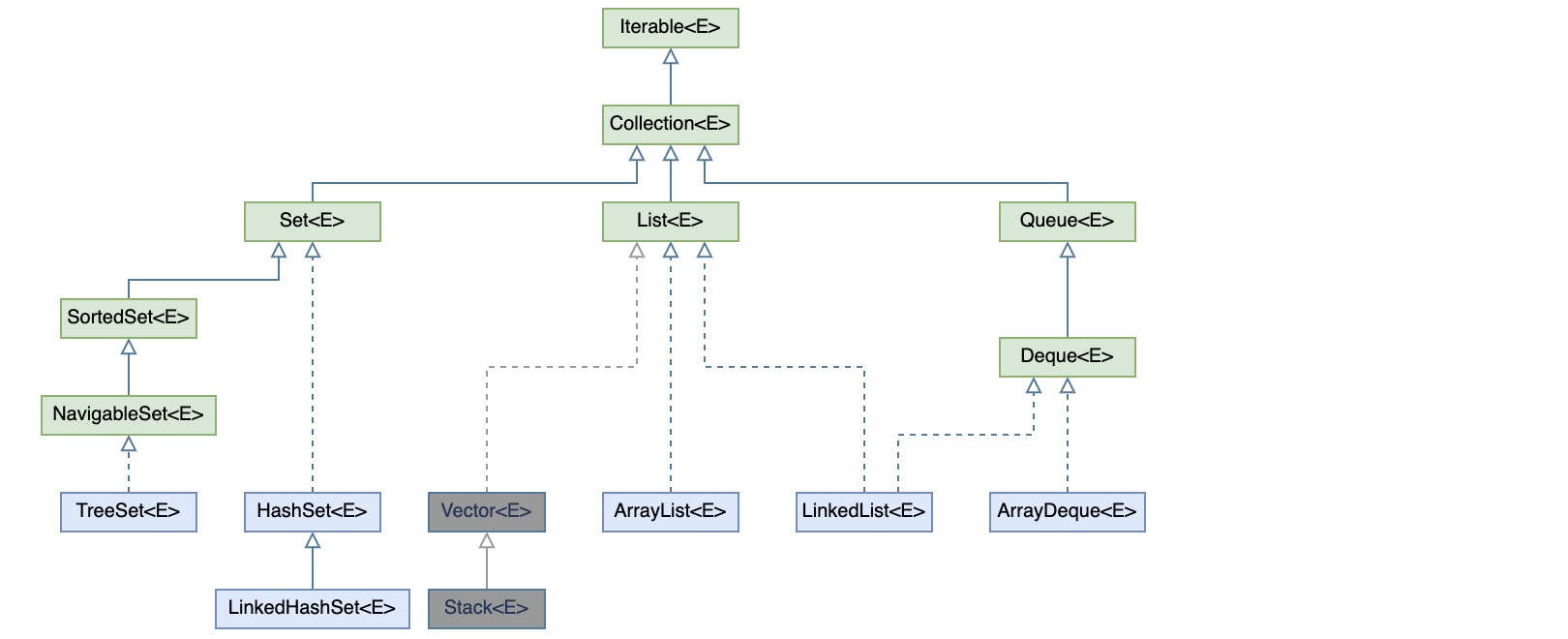
其中Vector和Stack灰色表示其已经被废弃，保留至今除了兼容早期已经使用了这两个类的应用之外，应该只剩纪念意义了；
TreeSet其实是树结构，不过它实现了Collection接口，刚好弥补了其它实现类没有的按照大小排序的能力；
HashSet其实是个散列表集合，不过子类LinkedHashSet在其基础上维护了一个链表结构；
ArrayList和ArrayDeque分别是数组实现的列表和队列；
LinkedList则是使用链表同时实现了列表和队列，如果需要，也完全可以代替Stack当成栈使用。

3. SortedArrayList

线性数据结构有一个问题：如果想从列表中寻找一个特定的元素，那么免不了要进行遍历，其时间复杂度将是O(N)。不过如果是有序的，那么便可以用二分法将查找的复杂度降为 $O(\log_{2} {n})$

上面类图中，只有TreeSet拥有排序的特性，但其限制了元素不可重复，其它类最多只是维护了插入的先后顺序，想按照大小排序则需要借助Collections工具自己手动排下序。因此，我们可以自己添加这样一个列表：每次添加或删除之后维持列表的有序。

至于实现，肯定不会基于LinkedList，因为它的元素没有下标，使用二分法每次要想获取中间元素，都要先进行遍历，这显然得不偿失，所以只能借助ArrayList了，但是ArrayList在设计上并没有考虑给让别人扩展，所以除了用二分法修改indexOf(Object o)和add(E e)两个方法外，其它代码基本都要复制一遍。

:https://github.com/shanhm1991/Echo/blob/master/src/main/java/io/github/echo/structure/SortedArrayList.java

public class SortedArrayList<E extends Comparable<? super E>> implements List<E>{

    // ...

    private boolean asc;

    @Override
    public int indexOf(Object o) {
        if(size == 0){
            return -1;
        }

        E e = (E)o;
        if(e.compareTo((E)elementData[0]) == 0){
            return 0;
        }

        int index = -1;

        int left = 0;
        int right = size - 1;
        int middle = (left + right) / 2;
        while(middle != left){
            if(e.compareTo((E)elementData[middle]) == 0){
                index = middle;
                break;
            }
            if(asc == e.compareTo((E)elementData[middle]) < 0){
                right = middle;
                middle = (left + right) / 2;
            }else if(asc == e.compareTo((E)elementData[middle]) > 0){
                left = middle;
                middle = (left + right) / 2;
            }
        }

        if(index == -1){
            return -1;
        }
        while(e.compareTo((E)elementData[--index]) == 0);
        return ++index;
    }

    @SuppressWarnings("unchecked")
    @Override
    public boolean add(E e) {
        ensureCapacityInternal(size + 1);
        if(size == 0){
            elementData[0] = e;
            size++;
            modCount++;
            return true;
        }

        int left = 0;
        int right = size - 1;
        if(e.compareTo((E)elementData[left]) == 0){
            System.arraycopy(elementData, 0, elementData, 1, size);
            elementData[0] = e;
        }else if(e.compareTo((E)elementData[right]) == 0){
            elementData[right + 1] = e;
        }else if(asc == e.compareTo((E)elementData[left]) < 0){
            System.arraycopy(elementData, 0, elementData, 1, size);
            elementData[0] = e;
        }else if(asc == e.compareTo((E)elementData[right]) > 0){
            elementData[right + 1] = e;
        }else{
            int middle = (left + right) / 2;
            while(e.compareTo((E)elementData[middle]) != 0 && middle != left){
                if(asc == e.compareTo((E)elementData[middle]) < 0){
                    right = middle;
                    middle = (left + right) / 2;
                }else if(asc == e.compareTo((E)elementData[middle]) > 0){
                    left = middle;
                    middle = (left + right) / 2;
                }
            }
            int index = middle + 1; 
            System.arraycopy(elementData, index, elementData, index + 1, size - index);
            elementData[index] = e;
        }

        size++;
        modCount++;
        return true;
    }
    
    // ...
}