定义:Avl树在二叉查找树的基础上加了一个平衡条件:对于任意节点,其左右子树的高度差最多为1。
1. 旋转
Avl树也是一颗二叉树,因此它的查找、插入和删除以及迭代都可以复用查找二叉树的实现。区别在于插入和删除操作之后需要恢复平衡,那么给每个节点记一个高度属性height,平衡的目标就是保证任意节点左右子节点的height差不超过1,而平衡的手段则是旋转。
首先根据旋转方向,可以将旋转分为 左旋 和 右旋,根据二叉查找树的性质,可以画出如下示意图:

可以看出,右旋转会将左子树的高度减一而右子树的高度加一,左旋转则相反。因此,可以通过旋转来调节左右子树的高度,对于图中的节点,可以确定K2 < B < K1
如果右旋转,则旋转的动作是让K2上升,K1下沉,使K1成为K2的右子树,并将K2的原右子树B变为K1的左子树;
如果左旋转,则是让K1上升,K2下沉,使K2替换K1的左子树,并将K1的原左子树B变为K2的右子树;
另外,可以看出每次旋转只需要重新计算K1和K2的高度,而对其他节点没有任何影响。
由于每个节点最多有两个儿子,因此针对需要重新平衡的节点,可以将需要旋转的情形分为4种:
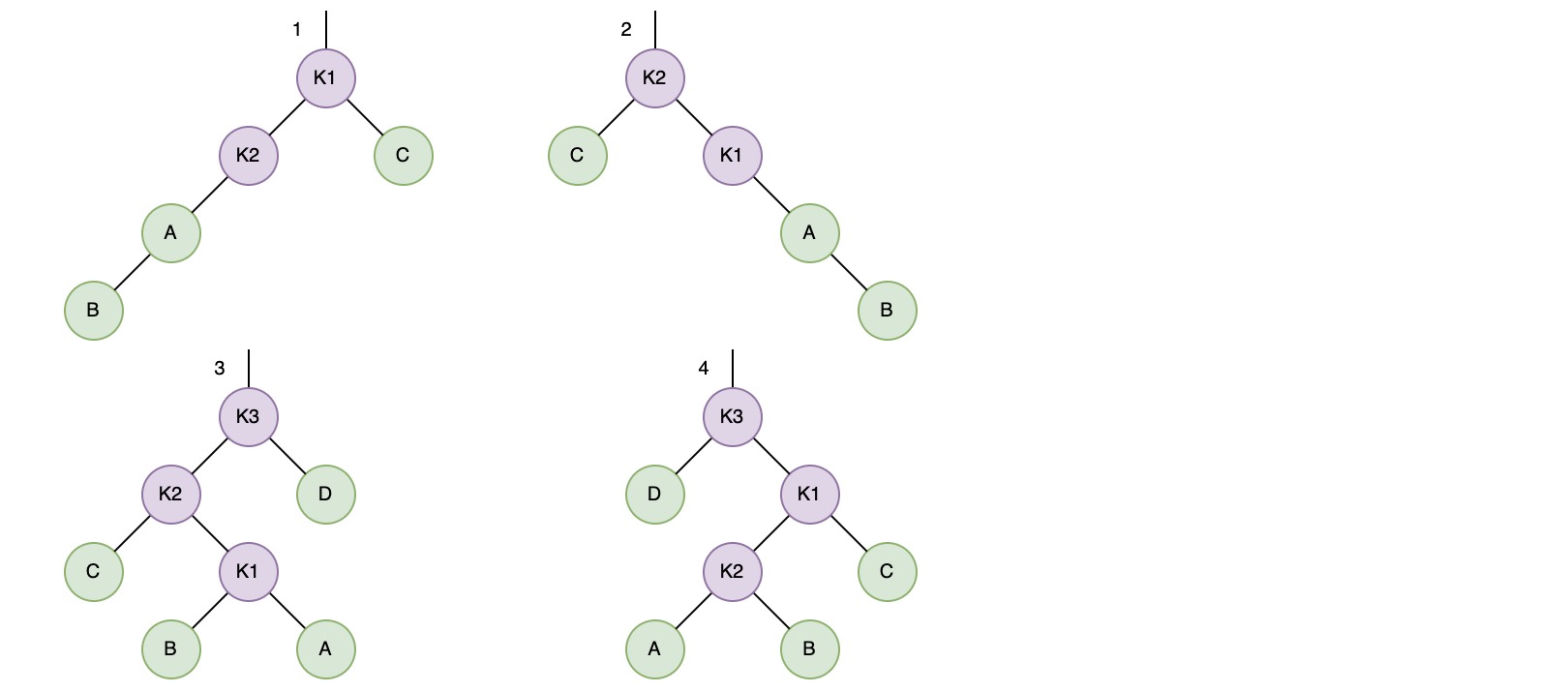
1 和 2 是对称的两种情形,需要调整的是左-左子树,或者右-右子树,通过一次 单旋转 即可恢复平衡;
3 和 4 也是对称的,但需要调整的是左-右子树,或者右-左子树,由于较深的子树处于树结构的中间,这时仅用单旋转并不能解决问题,而是需要通过 双旋转 才能恢复平衡,思路就是将深度过深的树从内侧转移到外侧,这样就可以将情形3和4转化成情形1或2
以情形 4 为例:可以先对右子树的 k1-k2 两个节点进行一次右旋转,然后再对 K2-K3 进行一次左旋转以达到重新平衡。
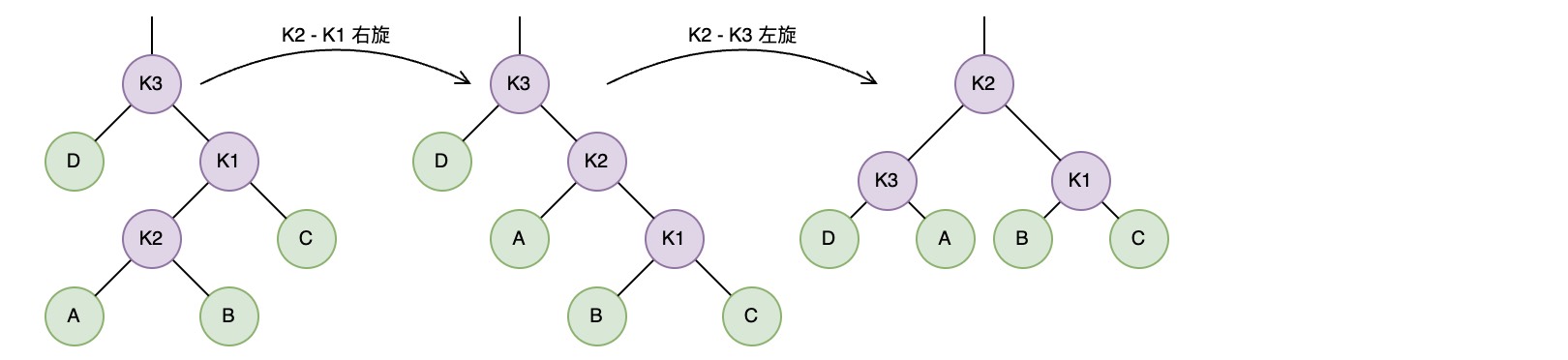
2. 示例
问题:依次插入10, 11, 9, 5, 2, 1, 6, 8,然后删除1
在插入节点2之后,将会在节点9上检测到不平衡,需要一次右旋转来恢复平衡
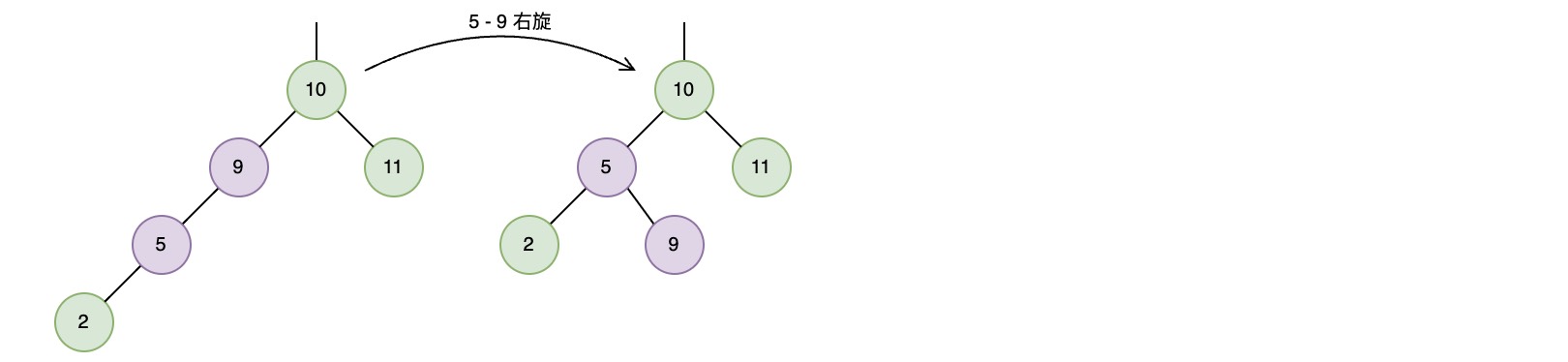
接着在插入节点1之后,将会在节点10上检测到不平衡,需要一次右旋转来恢复平衡
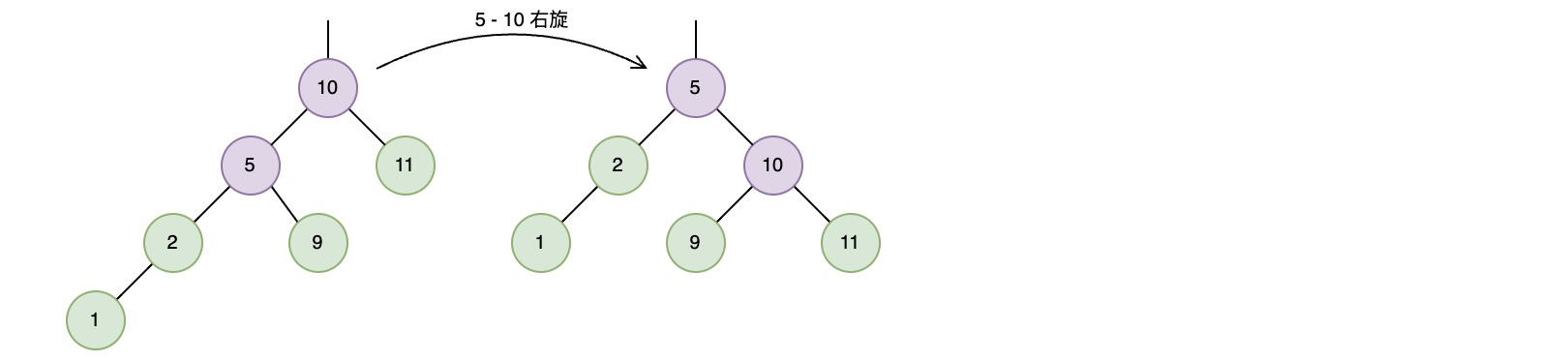
在连续插入节点6和8之后,将会在节点9上检测到不平衡,需要一个左-右双旋转来恢复平衡
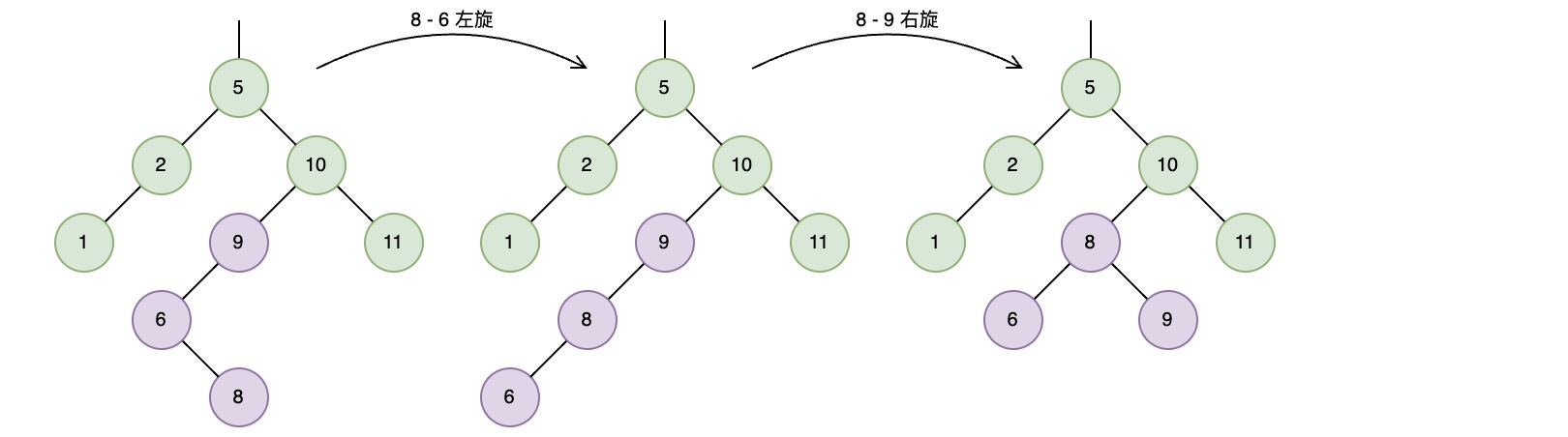
而在删除节点1后,将会在根节点5上检测到不平衡,需要一个右-左双旋转来恢复平衡
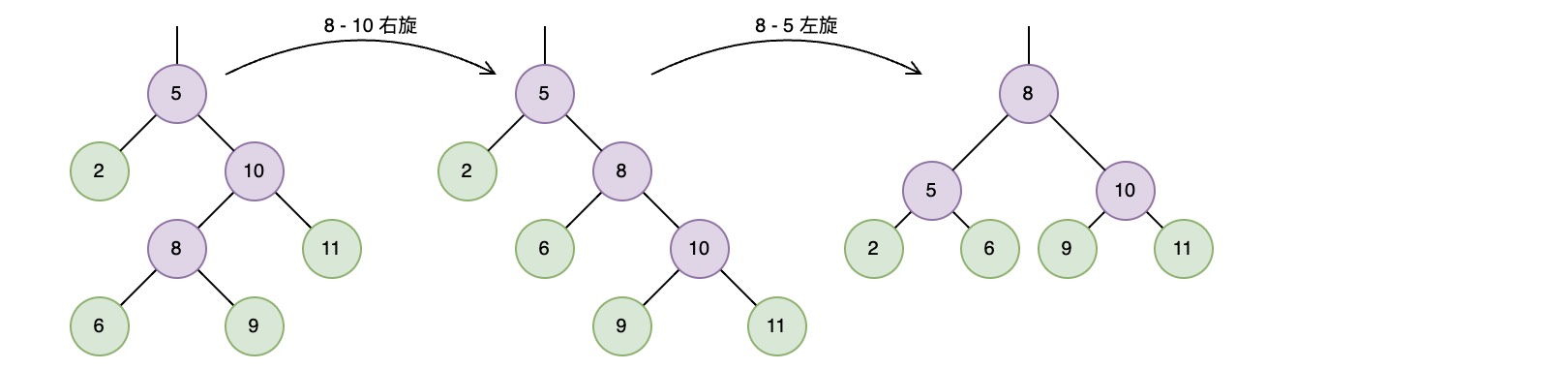
3. java实现
可以继承前面二叉树的实现,重写一下插入和删除,提供一个Set实现
:https://github.com/shanhm1991/Echo/blob/master/src/main/java/io/github/echo/structure/tree/AvlTreeSet.java mark:63,64,65,73,74,751
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
| public class AvlTreeSet<E extends Comparable<? super E>> extends BinaryTreeSet<E> {
private static final int ALLOWED_IMBALANCE = 1;
private AvlNode<E> root;
@Override
protected AvlNode<E> getRoot() {
return root;
}
@Override
public void clear() {
root = null;
size = 0;
}
@Override
public boolean add(E o){
root = add(o, getRoot());
return true;
}
private AvlNode<E> add(E e, AvlNode<E> node) {
if(node == null){
size++;
return new AvlNode<>(e);
}
int compare = e.compareTo(node.element);
if(compare < 0){
node.left = add(e, (AvlNode<E>)node.left);
}else if(compare > 0){
node.right = add(e, (AvlNode<E>)node.right);
}else{
node.element = e;
}
return balance(node);
}
private AvlNode<E> balance(AvlNode<E> node) {
if(node == null){
return node;
}
if(getHeight(node.left) - getHeight(node.right) > ALLOWED_IMBALANCE){
if(getHeight(node.left.left) >= getHeight(node.left.right)){
node = rotateRight(node);
}else{
node = rotateLeftRight(node);
}
}else if(getHeight(node.right) - getHeight(node.left) > ALLOWED_IMBALANCE){
if(getHeight(node.right.right) >= getHeight(node.right.left)){
node = rotateLeft(node);
}else{
node = rotateRightLeft(node);
}
}
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
return node;
}
private AvlNode<E> rotateRight(AvlNode<E> node) {
AvlNode<E> leftNode = (AvlNode<E>)node.left;
node.left = leftNode.right;
leftNode.right = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
leftNode.height = Math.max(getHeight(leftNode.left), node.height) + 1;
return leftNode;
}
private AvlNode<E> rotateLeft(AvlNode<E> node) {
AvlNode<E> rightNode = (AvlNode<E>)node.right;
node.right = rightNode.left;
rightNode.left = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
rightNode.height = Math.max(getHeight(rightNode.right), node.height) + 1;
return rightNode;
}
private AvlNode<E> rotateLeftRight(AvlNode<E> node) {
node.left = rotateLeft((AvlNode<E>)node.left);
return rotateRight(node);
}
private AvlNode<E> rotateRightLeft(AvlNode<E> node) {
node.right = rotateRight((AvlNode<E>)node.right);
return rotateLeft(node);
}
private int getHeight(Node<E> node) {
AvlNode<E> avlNode = (AvlNode<E>)node;
return avlNode == null ? -1 : avlNode.height;
}
@SuppressWarnings("unchecked")
@Override
public boolean remove(Object o){
root = remove((E)o, getRoot());
return true;
}
private AvlNode<E> remove(E e, AvlNode<E> node) {
if(node == null) {
return node;
}
int compare = e.compareTo(node.element);
if(compare < 0){
node.left = remove(e, (AvlNode<E>)node.left);
}else if(compare > 0){
node.right = remove(e, (AvlNode<E>)node.right);
}else if(node.left != null && node.right != null){
node = (AvlNode<E>)removeLeftMax(node);
size--;
}else{
node = (node.left != null) ? (AvlNode<E>)node.left : (AvlNode<E>)node.right;
size--;
}
return balance(node);
}
static class AvlNode<E> extends Node<E> {
int height = 0;
AvlNode(E e) {
super(e);
}
@Override
public String toString() {
return super.toString();
}
}
}
|
4. Avl树的高度
对于节点数为 $N$,高度为 $H$ 的Avl树:最好的情形与查找二叉树一样,即一颗满二叉树:$H = \log_{2} {(N+1)}$ ,再看最差的情形,即满足Avl树规则的同时拥有最少的节点数,考虑如下这种极端情形:每个节点的右子树刚好比左子树高1
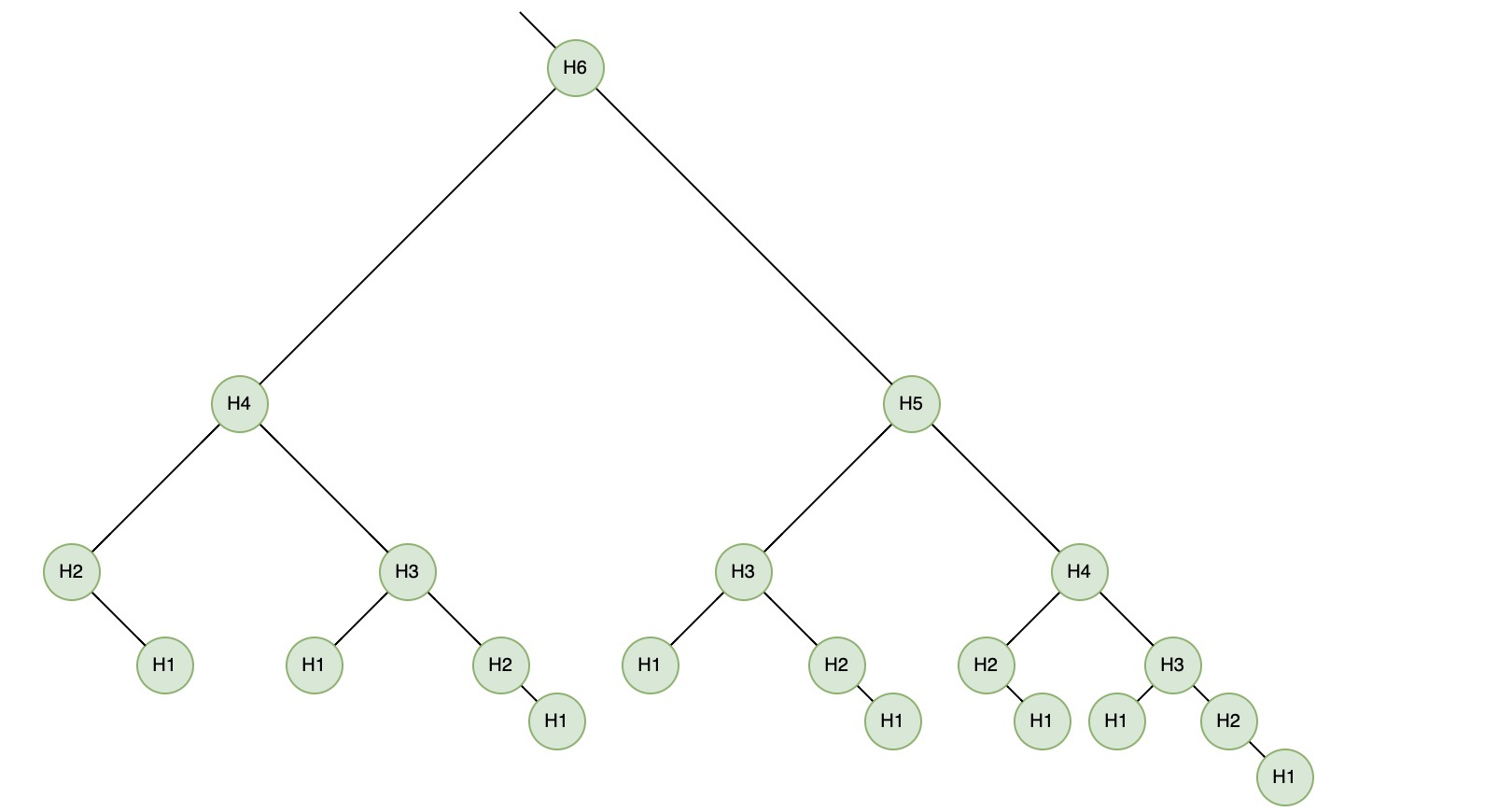
那么可以看出如下规律,假设 $N$ 层的Avl树的节点数之和为 $S_n$,那么有:
$S_1 = 1;$
$S_2 = 2;$
$S_3 = S_2 + S_1 + 1;$
$S_4 = S_3 + S_2 + 1;$
$S_5 = S_4 + S_3 + 1;$
$S_6 = S_5 + S_4 + 1;$
$…$
$S_n=S_{n-1} + S_{n-2} + 1;$
看上去有点像一个斐波那契数列:$a_n = a_{n-1} + a_{n-2}$,其通项为:$a_n=\frac{((1 + \sqrt 5)/2)^n - ((1 - \sqrt 5)/2)^n} {\sqrt 5}$
这里其实是想知道Avl的求和公式,但是自己也没有能力去证明了,不过可以从维基上查到:$H = S_n = \log_{2} {(\sqrt 5 \times (N+1))} - 2$
参考:
- 《算法导论》
- 《数据结构与算法分析》







