数据结构 2-3树
words: 1.3k views: time: 4min前面已经讨论过平衡二叉树Avl,其目的就是通过旋转尽量使树保持平衡,以降低树的高度或查找的时间复杂度。当然,最好的情形是能转化成一颗满二叉树,使树的高度与节点数完全满足 $H = \log_{2} {(n+1)}$,但实际在大部分情形下,无论其如何旋转调整都无法做到,毕竟对于每个节点,其最多只能有一个元素,两个子节点。
既然如此,那就打破规则,允许一个节点最多拥有两个元素,三个子树,这样就不再存在一个节点只有单个子树的情况,取而代之的是节点是二叉还是三叉(如果一个节点只有单个子树,就使其成为三叉节点),这也就是 2-3 树的字面意思:即同时拥有二叉节点和三叉节点的树, 这样在插入删除时就可以自下而上采取分裂合并的方式保证所有叶子节点都在同一层,并使树的节点达到一个绝对平衡的状态。
2-3 树本身并没有什么实际使用场景,但其在思路上打破了二叉树的约束,在树形数据结构中起着一个关键的连接作用,它解决了Avl树无法绝对平衡的问题,并且顺着这个思路可以进一步联想到红黑树以及后面要讲的B树。
1. 定义
这个网上有很多,可以在维基上找到,这里简要描述下:
- 2-3树要么为空要么具有以下性质;
- 对于二叉节点,有一个元素和两个子树,子树要么为空,要么也是一个2-3树,当前节点的元素大于左子树所有元素,并小于右子树所有元素;
- 对于三叉节点,有两个元素A, B和三个子树,左子树中所有元素小于A,中子树中所有元素大于A而小于B ,右子树中所有元素大于B;
其实2-3树本质上是一个阶为 3 的 B树,后面在讨论B树时再用更通用的描述来进行定义
2. 分析实现
2.1 插入
继承二叉树的性质,插入肯定都是从树叶开始,可以先将元素往树叶节点中进行追加,如果树叶节点超过三叉,即元素达到三个,就对其进行分裂,并将中间的元素合并到父节点,同时将分裂出来的左右元素作为中间元素的左右子树,如果合并到父节点之后导致父节点也超过了三叉,那么就继续递归对父节点进行相同的处理,直到满足规则为止。
- 示例
依次插入10,11,9,5,2,6,8,15,16,12,17
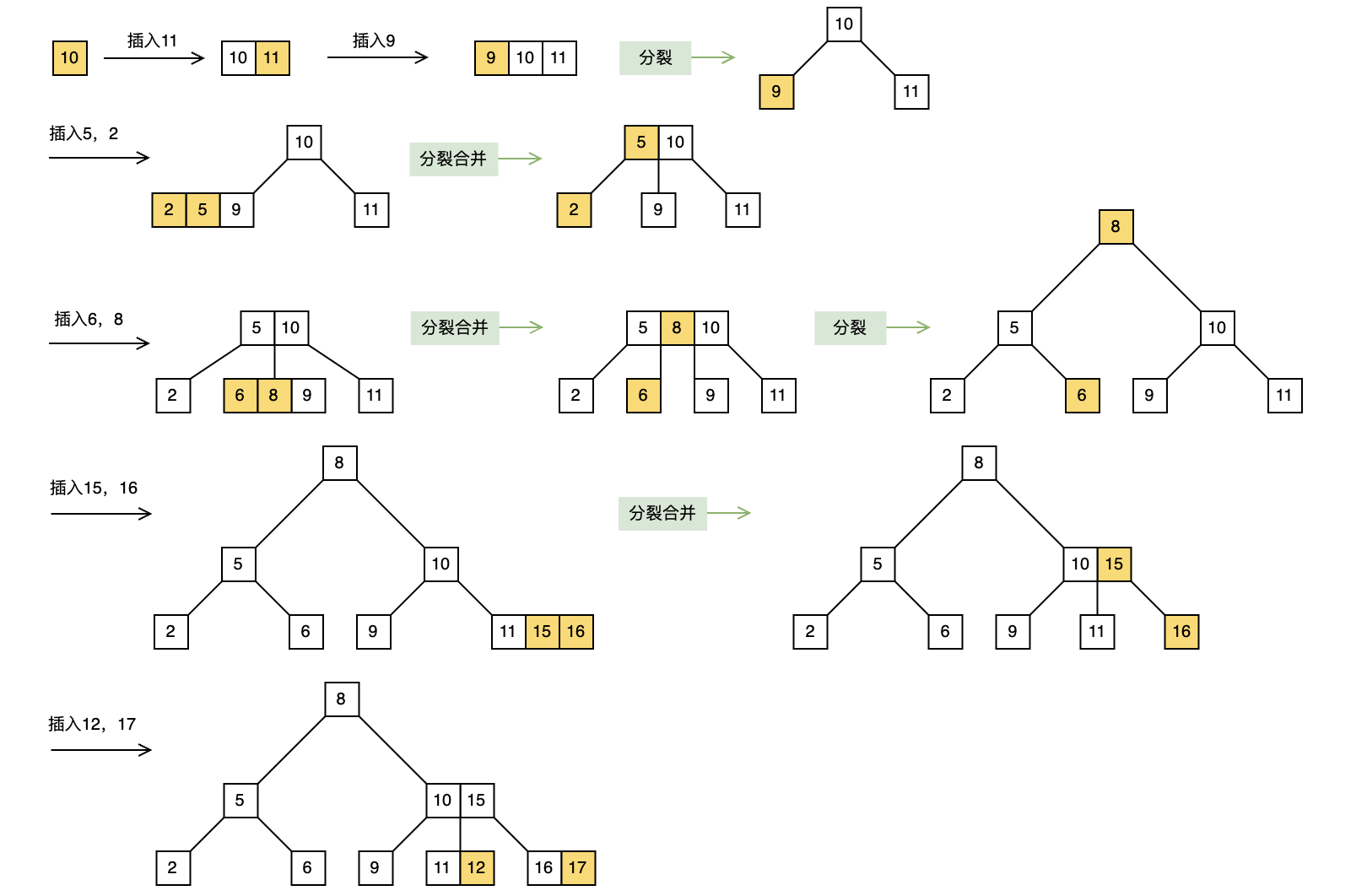
2.2 删除
还是与之前讨论一样,先转化为对树叶的删除,如果树叶是三叉节点,则直接删除结束,否则再其兄弟节点和父弟节点的不同情形分别讨论,这里接着上面的插入的示例,在其基础上进行删除操作。
1.树叶本身是三叉节点

2.兄弟节点为三叉,父节点为二叉

3.兄弟节点为二叉,父节点为三叉

4.兄弟节点和父节点都为二叉

向上递归处理时,父节点的情形不一定与树叶一样,比如在上面删除15之前删除2,那么父节点就可以像兄弟节点借取

3. 2-3树与红黑树
2-3树解决了Avl树无法达到绝对平衡的问题,但是要想用代码把它描述出来会显得有些臃肿,于是有人想到了可以在二叉树的基础上附加一些规则,使其与2-3树能达到等价的效果。
由于2-3树的节点是绝对平衡的,并且每个节点至多拥有两个关键字。于是我们可以约定:每个节点必须有且仅有一个黑色节点,如果存在另一个节点则标记成红色,那么由这些黑色节点构成的就是一颗绝对平衡的满二叉树
如果对红黑树比较熟悉,上面这个约定基本就可以翻译成红黑树的定义:数据结构. 红黑树
复用上面的示例,下面来将其中所有的元素都涂成红色或者黑色,并保证任意节点中有且仅有一个黑色元素,那么将会发现,在任何一次插入删除完成之后,都可以将结果等价成一颗红黑树
- 插入
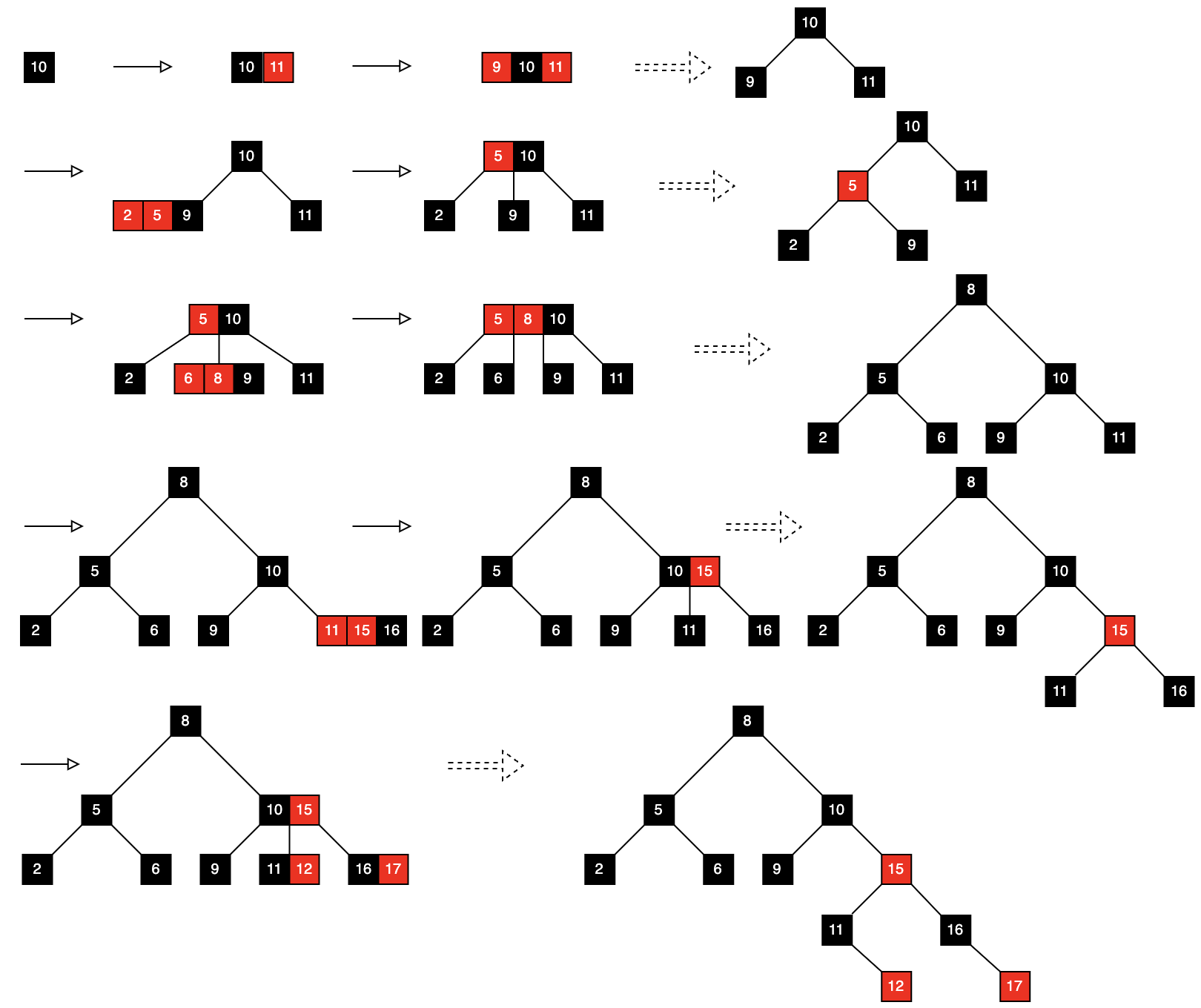
- 删除
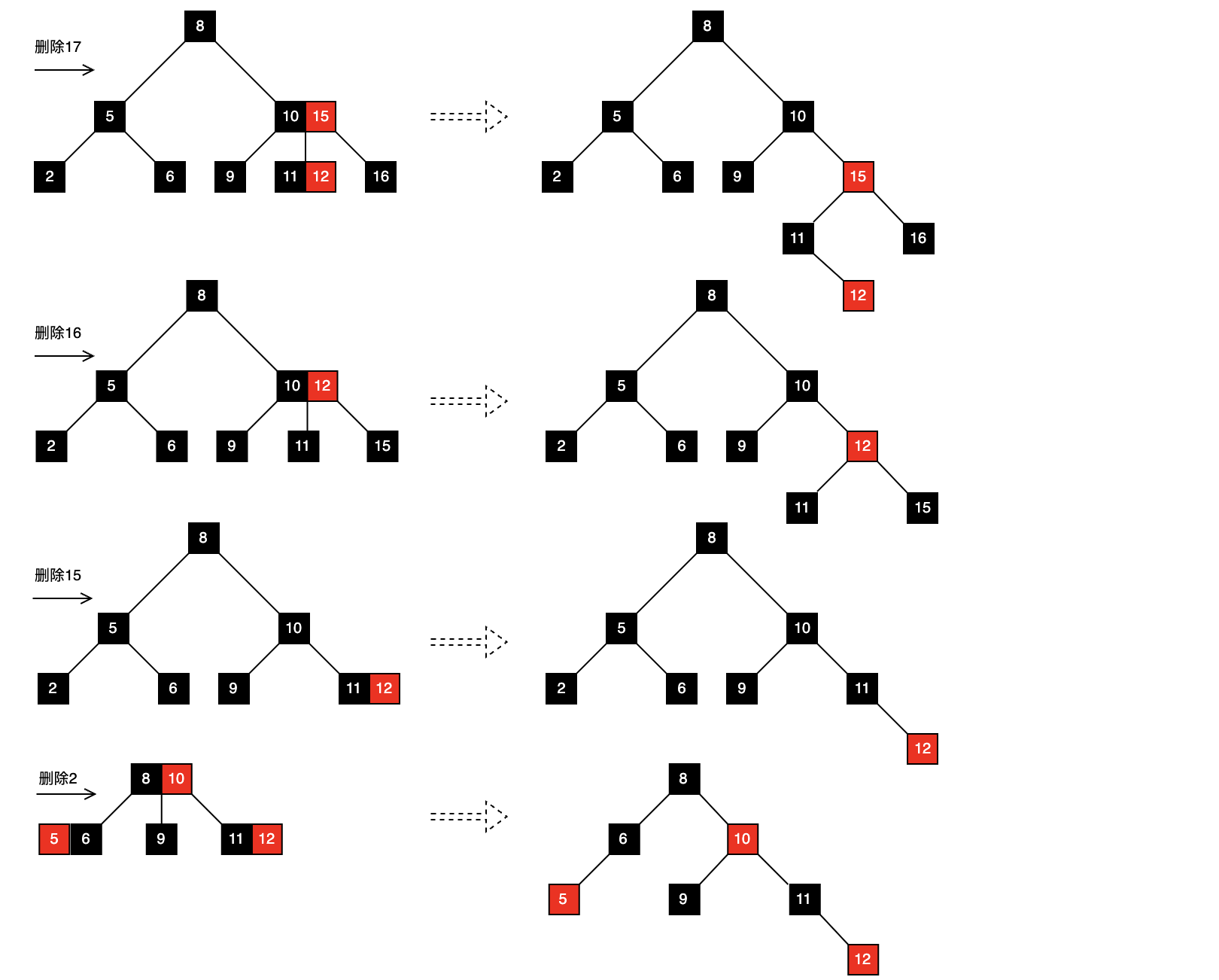
4. 2-3树与B树
上面已经提过,2-3树本质就是阶为3就B树,这里不再赘述。
参考: